The subchapter 3.5 of Bayesian Data Analysis Third Edition gives distributional results of Bayesian inference for the parameters of a multivariate normal distribution with a known variance. Additionally, this article discusses the derivation of those results (Equation 3.13 of the book) in gory details.
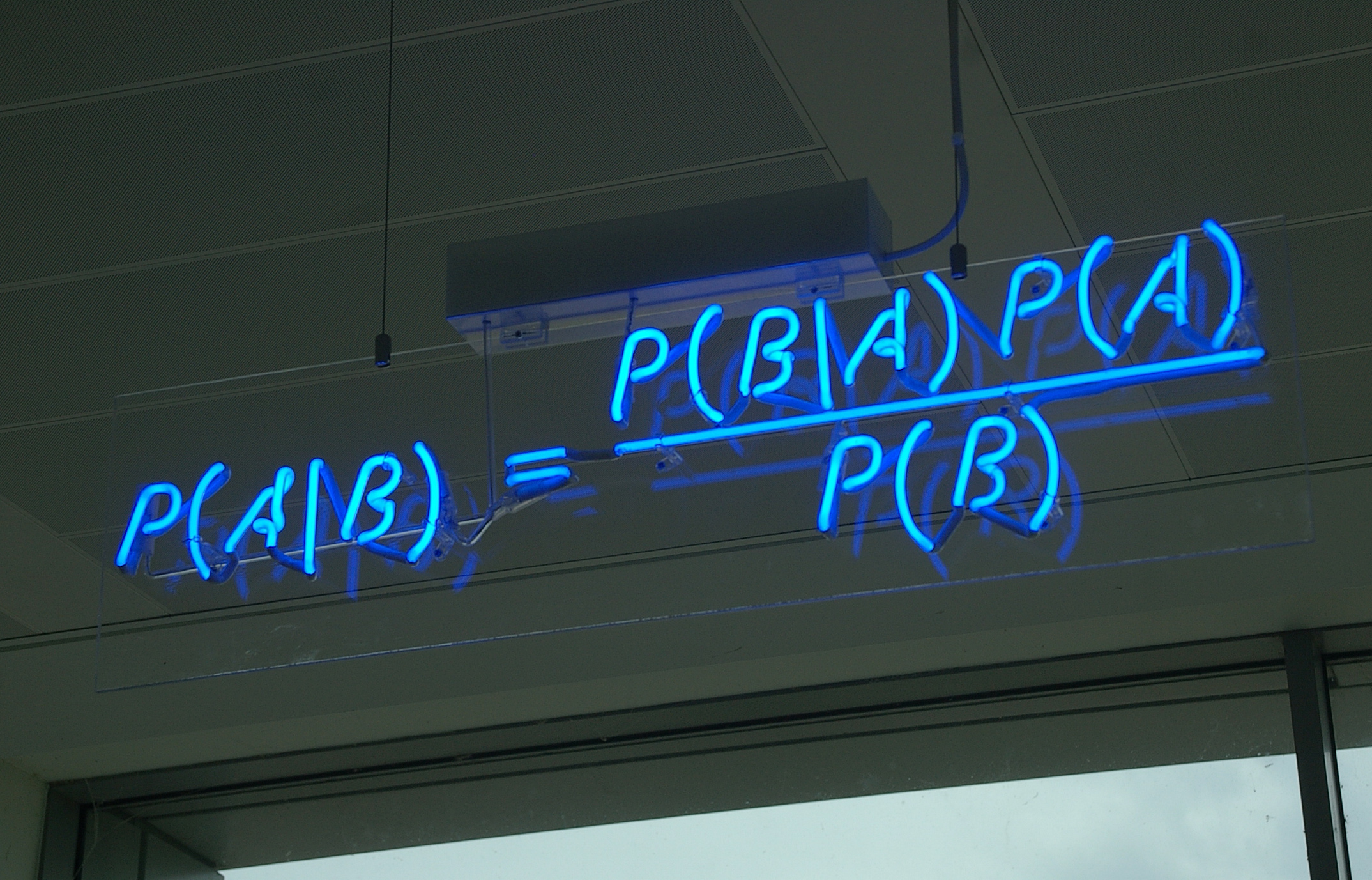
Suppose we have a model for an observable vector $y$ of $d$ components, that is $y$ is a column vector of $d \times 1$, with the multivariate normal distribution,
\[\begin{equation} y \mid \mu, \Sigma \sim \text{N}(\mu, \Sigma) \tag{1}\label{eq:mvn-one-sample} \end{equation}\]where $\mu$ is a column vector of length $d$ and $\Sigma$ is a known $d \times d$ variance matrix, which is symmetric and positive definite. Therefore, the likelihood function for a single observation is
\[\begin{equation} \Pr(y \mid \mu, \Sigma) \propto \lvert \Sigma \rvert^{-1/2} \exp \left( - \frac{1}{2} (y-\mu)^T \Sigma^{-1} (y - \mu) \right), \tag{2}\label{eq:likelihood-one-sample} \end{equation}\]and for a sample of $n$ independent and identically distributed observations, $y_1, \ldots, y_n$, is
\[\begin{align} \Pr( y_1, \ldots, y_n \mid \mu, \Sigma ) &\propto \prod_{i=1}^{n}{ \Pr( y_i \mid \mu, \Sigma ) } \tag{3}\label{eq:likelihood-samples-1} \\ &= \prod_{i=1}^{n}{ \lvert \Sigma \rvert^{-1/2} \exp \left( - \frac{1}{2} (y_i-\mu)^T \Sigma^{-1} (y_i - \mu) \right) } \tag{4}\label{eq:likelihood-samples-2} && \text{using Equation }\eqref{eq:likelihood-one-sample} \\ &= \prod_{i=1}^{n}{ \lvert \Sigma \rvert^{-1/2} } \prod_{i=1}^{n}{\exp \left( - \frac{1}{2} (y_i-\mu)^T \Sigma^{-1} (y_i - \mu) \right) } \tag{5}\label{eq:likelihood-samples-3} \\ &= \lvert \Sigma \rvert^{-n/2} \exp \left( - \frac{1}{2} \sum_{i=1}^{n}{(y_i-\mu)^T \Sigma^{-1} (y_i - \mu)} \right). \tag{6}\label{eq:likelihood-samples-4} \\ \end{align}\]Actually, given the following nice trace property,
\[\begin{equation} \sum_{i=1}^{n}{x_i^T A x_i} = \text{tr}\left( A \sum_{i=1}^{n}{x_i x_i^T} \right) \tag{7}\label{eq:trace-property} \end{equation}\]with $x_i$ is a column vector whose dimension is $d \times 1$, $A$ is a symmetric matrix whose dimension is $d \times d$, and $\text{tr}$ is a trace function, we can rewrite Equation \eqref{eq:trace-property} as follows:
\[\begin{equation} \Pr( y_1, \ldots, y_n \mid \mu, \Sigma ) \propto \lvert \Sigma \rvert^{-n/2} \exp \left( -\frac{1}{2} \text{tr}(\Sigma^{-1} S_0) \right) \tag{8}\label{eq:likelihood-final-version} \end{equation}\]where $S_0$ is the “sums squares” matrix relative to $\mu$,
\[\begin{equation} S_0 = \sum_{i=1}^{n}{(y_i - \mu)(y_i - \mu)^T}. \tag{9}\label{eq:sum-of-squares} \end{equation}\]Before we construct the posterior distribution of the model, let’s define the prior distribution as follows:
\[\begin{equation} \Pr( \mu ) \propto \lvert \Lambda_0 \rvert^{-1/2} \exp \left(-\frac{1}{2} (\mu - \mu_0)^T \Lambda_0^{-1} (\mu - \mu_0) \right) \tag{10}\label{eq:prior} \end{equation}\]that is $\mu \sim \text{N}(\mu_0, \Lambda_0)$. By the way, $\Lambda_0$ is also a symmetric and positive definite matrix as well.
\[\begin{align} \Pr( \mu \mid y, \Sigma ) &\propto \Pr( y \mid \mu, \Sigma ) \Pr(\mu \mid \Sigma) && \text{by Bayes rule} \tag{11}\label{eq:posterior-def} \\ &= \lvert \Sigma \rvert^{-n/2} \exp \left( - \frac{1}{2} \sum_{i=1}^{n}{(y_i-\mu)^T \Sigma^{-1} (y_i - \mu)} \right) \times \lvert \Lambda_0 \rvert^{-1/2} \exp \left(-\frac{1}{2} (\mu - \mu_0)^T \Lambda_0^{-1} (\mu - \mu_0) \right) \\ &\propto \exp \left( -\frac{1}{2} \underbrace{ \left( (\mu - \mu_0)^T \Lambda_0^{-1} (\mu - \mu_0) + \sum_{i=1}^{n}{(y_i-\mu)^T \Sigma^{-1} (y_i - \mu)} \right)}_{\text{A}} \right) \tag{12}\label{eq:posterior-1} \end{align}\]Now that we have both likelihood and prior distributions; let’s compute the posterior distribution of the model,
Part $\text{A}$ in Equation \eqref{eq:posterior-1} is actually a “completing the quadratic form” problem.
Let’s solve the problem as follows:
\[\begin{align} \text{A} &= (\mu^T - \mu_0^T) \Lambda_0^{-1} (\mu - \mu_0) + \sum_{i=1}^{n}{(y_i^T - \mu^T)\Sigma^{-1}(y_i - \mu)} && \text{by transpose property} \tag{13}\label{eq:complete-squares-1} \\ &= \underbrace{(\mu^T \Lambda_0^{-1} - \mu_0^T \Lambda_0^{-1}) (\mu - \mu_0)}_{\text{B}} + \underbrace{\sum_{i=1}^{n}{(y_i^T \Sigma^{-1} - \mu^T \Sigma^{-1})(y_i - \mu)}}_{\text{C}} \tag{14}\label{eq:complete-squares-2} \end{align}\]Let’s multiply out all terms in part $\text{B}$ in Equation \eqref{eq:complete-squares-2} as follows:
\[\begin{align} \text{B} &= \mu^T \Lambda_0^{-1} \mu - \underbrace{\mu^T \Lambda_0^{-1} \mu_0}_{\text{a scalar}} - \underbrace{\mu_0^T \Lambda_0^{-1} \mu}_{\text{a scalar}} + \mu_0^T \Lambda_0^{-1} \mu_0 \tag{15}\label{eq:b-1} \\ &= \mu^T \Lambda_0^{-1} \mu - \mu^T \Lambda_0^{-1} \mu_0 - (\mu^T \Lambda_0^{-1} \mu_0)^T + \mu_0^T \Lambda_0^{-1} \mu_0 && \text{by transpose property} \tag{16}\label{eq:b-2} \\ &= \mu^T \Lambda_0^{-1} \mu - \mu^T \Lambda_0^{-1} \mu_0 - \mu^T \Lambda_0^{-1} \mu_0 + \mu_0^T \Lambda_0^{-1} \mu_0 && \text{as } \mu^T \Lambda_0^{-1} \mu_0 = (\mu^T \Lambda_0^{-1} \mu_0)^T \tag{17}\label{eq:b-3} \\ &= \mu^T \Lambda_0^{-1} \mu - 2 \mu^T \Lambda_0^{-1} \mu_0 + \mu_0^T \Lambda_0^{-1} \mu_0. \tag{18}\label{eq:b-4} \\ \end{align}\]Let’s also multiply out part $\text{C}$ in Equation \eqref{eq:complete-squares-2},
\[\begin{align} \text{C} &= \sum_{i=1}^{n}{(y_i^T \Sigma^{-1} y_i - \underbrace{y_i^T \Sigma^{-1} \mu}_{\text{scalar}} - \underbrace{\mu^T \Sigma^{-1} y_i}_{\text{scalar}} + \mu^T \Sigma^{-1} \mu)} \tag{19}\label{eq:c-1} \\ &= \sum_{i=1}^{n}{(y_i^T \Sigma^{-1} y_i - (\mu^T \Sigma^{-1} y_i)^T - \mu^T \Sigma^{-1} y_i + \mu^T \Sigma^{-1} \mu)} && \text{by transpose property} \tag{20}\label{eq:c-2} \\ &= \sum_{i=1}^{n}{(y_i^T \Sigma^{-1} y_i - \mu^T \Sigma^{-1} y_i - \mu^T \Sigma^{-1} y_i + \mu^T \Sigma^{-1} \mu)} && \text{as } (\mu^T \Sigma^{-1} y_i)^T = \mu^T \Sigma^{-1} y_i \tag{21}\label{eq:c-3} \\ &= \sum_{i=1}^{n}{(y_i^T \Sigma^{-1} y_i - 2 \mu^T \Sigma^{-1} y_i + \mu^T \Sigma^{-1} \mu)} \tag{22}\label{eq:c-4} \\ &= \sum_{i=1}^{n}{y_i^T \Sigma^{-1} y_i} - \sum_{i=1}^{n}{2 \mu^T \Sigma^{-1} y_i} + \sum_{i=1}^{n}{\mu^T \Sigma^{-1} \mu} && \text{by a linear operator of }\sum \tag{23}\label{eq:c-5} \\ &= \sum_{i=1}^{n}{y_i^T \Sigma^{-1} y_i} - 2 \mu^T \Sigma^{-1} \sum_{i=1}^{n}{y_i} + \sum_{i=1}^{n}{\mu^T \Sigma^{-1} \mu} \tag{24}\label{eq:c-6}\\ &= \sum_{i=1}^{n}{y_i^T \Sigma^{-1} y_i} - 2 \mu^T \Sigma^{-1} n \overline{y} + \sum_{i=1}^{n}{\mu^T \Sigma^{-1} \mu} && \text{as }\overline{y} = \frac{\sum_{i=1}^n y_i}{n} \tag{25}\label{eq:c-7} \\ &= \sum_{i=1}^{n}{y_i^T \Sigma^{-1} y_i} - 2 \mu^T \Sigma^{-1} n \overline{y} + n \mu^T \Sigma^{-1} \mu && \text{as }\sum_{i=1}^{n}{\text{constant}} = n \times \text{constant} \tag{26}\label{eq:c-8} \\ &= \sum_{i=1}^{n}{y_i^T \Sigma^{-1} y_i} - 2 \mu^T n \Sigma^{-1} \overline{y} + \mu^T n \Sigma^{-1} \mu \tag{27}\label{eq:c-9} \\ &= \mu^T n \Sigma^{-1} \mu - 2 \mu^T n \Sigma^{-1} \overline{y} + \sum_{i=1}^{n}{y_i^T \Sigma^{-1} y_i} && \text{just rearrange terms} \tag{28}\label{eq:c-10} \end{align}\]Now let’s combine both part $\text{B}$ (Equation \eqref{eq:b-4}) and part $\text{C}$ (Equation \eqref{eq:c-10}) into part $\text{A}$ in Equation \eqref{eq:complete-squares-2},
\[\begin{align} \text{A} =& \mu^T \Lambda_0^{-1} \mu - 2 \mu^T \Lambda_0^{-1} \mu_0 + \mu_0^T \Lambda_0^{-1} \mu_0 + \\ & \mu^T n \Sigma^{-1} \mu - 2 \mu^T n \Sigma^{-1} \overline{y} + \sum_{i=1}^{n}{y_i^T \Sigma^{-1} y_i} \tag{29}\label{eq:c-11} \\ =& \mu^T (\Lambda_0^{-1} + n \Sigma^{-1} ) \mu - 2 \mu^T ( \Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y} ) + \underbrace{\mu_0^T \Lambda_0^{-1} \mu_0 + \sum_{i=1}^{n}{y_i^T \Sigma^{-1} y_i}}_{\text{constant}_1} && \text{sum all terms accordingly} \tag{30}\label{eq:c-12} \\ =& \mu^T (\Lambda_0^{-1} + n \Sigma^{-1} ) \mu - 2 \mu^T ( \Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y} ) + \text{constant}_1 \tag{31}\label{eq:c-13} \\ =& \mu^T (\Lambda_0^{-1} + n \Sigma^{-1} ) \mu - \underbrace{\mu^T ( \Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y} )}_{\text{scalar}} - \underbrace{\mu^T ( \Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y} )}_{\text{scalar}} + \text{constant}_1 && \text{separate the middle term} \tag{32}\label{eq:c-14} \\ =& \mu^T (\Lambda_0^{-1} + n \Sigma^{-1} ) \mu - \mu^T ( \Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y} ) - ( \Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y} )^T \mu + \text{constant}_1 && \text{by transpose property} \tag{33}\label{eq:c-15} \\ =& \left( \mu^T (\Lambda_0^{-1} + n \Sigma^{-1} ) - (\Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y})^T \right) \left( \mu - (\Lambda_0^{-1} + n \Sigma^{-1})^{-1} (\Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y}) \right) \underbrace{- (\Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y})^T (\Lambda_0^{-1} + n \Sigma^{-1})^{-1} (\Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y}) + \text{constant}_1 }_{\text{constant}_2} && \text{by factoring & inverse matrix} \tag{34}\label{eq:c-16} \\ =& \left( \mu^T (\Lambda_0^{-1} + n \Sigma^{-1} ) - (\Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y})^T \right) \left( \mu - (\Lambda_0^{-1} + n \Sigma^{-1})^{-1} (\Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y}) \right) + \text{constant}_2 \tag{35}\label{eq:c-17} \\ =& \left( \mu^T - (\Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y})^T (\Lambda_0^{-1} + n \Sigma^{-1} )^{-1} \right) (\Lambda_0^{-1} + n \Sigma^{-1} ) \left( \mu - (\Lambda_0^{-1} + n \Sigma^{-1})^{-1} (\Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y}) \right) + \text{constant}_2 && \text{get }(\Lambda_0^{-1} + n \Sigma^{-1} ) \text{ out} \tag{36}\label{eq:c-18} \\ =& \left( \mu^T - (\Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y})^T (\Lambda_0^{-1} + n \Sigma^{-1} )^{-T} \right) (\Lambda_0^{-1} + n \Sigma^{-1} ) \left( \mu - (\Lambda_0^{-1} + n \Sigma^{-1})^{-1} (\Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y}) \right) + \text{constant}_2 && \text{symmetric property, }A^{-T} = A^{-1} \tag{37}\label{eq:c-19} \\ =& \left( \mu - (\Lambda_0^{-1} + n \Sigma^{-1} )^{-1} (\Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y}) \right)^T (\Lambda_0^{-1} + n \Sigma^{-1} ) \left( \mu - (\Lambda_0^{-1} + n \Sigma^{-1})^{-1} (\Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y}) \right) + \text{constant}_2 && \text{by transpose property} \tag{38}\label{eq:c-20} \\ =& \left( \mu - \mu_n \right)^T \Lambda_n^{-1} \left( \mu - \mu_n \right) + \text{constant}_2 \tag{39}\label{eq:c-21} \\ \end{align}\]where
\[\begin{align} \mu_n &= (\Lambda_0^{-1} + n \Sigma^{-1} )^{-1} (\Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y}) \text{ and} \nonumber \\ \Lambda_n^{-1} &= \Lambda_0^{-1} + n \Sigma^{-1}. \tag{40}\label{eq:final-mean-variance} \end{align}\]Next, let’s substitute the part $\text{A}$ (Equation \eqref{eq:c-21}) into the posterior distribution (Equation \eqref{eq:posterior-1}),
\[\begin{align} \Pr( \mu \mid y, \Sigma ) &\propto \exp \left( -\frac{1}{2} \underbrace{ \left( (\mu - \mu_0)^T \Lambda_0^{-1} (\mu - \mu_0) + \sum_{i=1}^{n}{(y_i-\mu)^T \Sigma^{-1} (y_i - \mu)} \right)}_{\text{A}} \right) \tag{41}\label{eq:posterior-2} \\ &= \exp \left( -\frac{1}{2} \left( \left( \mu - \mu_n \right)^T \Lambda_n^{-1} \left( \mu - \mu_n \right) + \text{constant}_2 \right) \right) \tag{42}\label{eq:posterior-3} \\ &= \exp \left( -\frac{1}{2} \left( \mu - \mu_n \right)^T \Lambda_n^{-1} \left( \mu - \mu_n \right) \right) \times \exp \left( \text{constant}_2 \right) \tag{43}\label{eq:posterior-4} \\ &\propto \exp \left( -\frac{1}{2} \left( \mu - \mu_n \right)^T \Lambda_n^{-1} \left( \mu - \mu_n \right) \right) \tag{44}\label{eq:posterior-5} \\ &= \text{N}(\mu \mid \mu_n, \Lambda_n) \tag{45}\label{eq:posterior-6} \end{align}\]where
\[\begin{align} \mu_n &= (\Lambda_0^{-1} + n \Sigma^{-1} )^{-1} (\Lambda_0^{-1} \mu_0 + n \Sigma^{-1} \overline{y}) \nonumber \\ \Lambda_n^{-1} &= \Lambda_0^{-1} + n \Sigma^{-1}. \nonumber \end{align}\]By the way, the above derivation is also mentioned as Exercise 3.13 in the book.
