Artikel ini hendak memberikan penjelasan yang lebih detil mengenai hubungan antara hasil kali titik (dot product) dengan sudut antara 2 vektor. Buku Larson (2016) pada halaman 235 kembali direkomendasikan menjadi referensi utama.

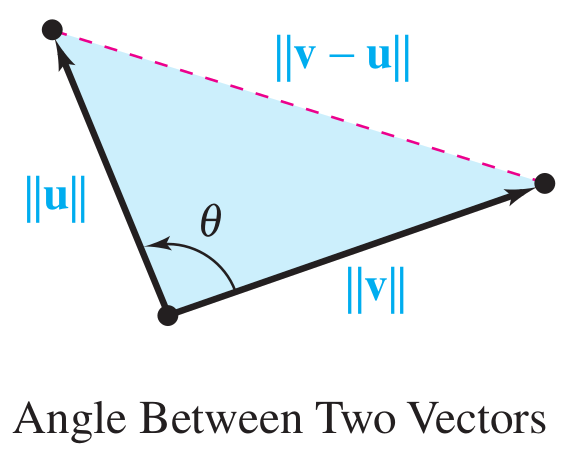
Diketahui dua buah vektor $\mathbf{u} = (u_1, u_2)$ dan $\mathbf{v} = (v_1, v_2)$ dan sudut $\theta$ adalah sudut yang dibentuk oleh vektor $\mathbf{u}$ dan $\mathbf{v}$ seperti pada gambar berikut:

Gambar di atas sepenuhnya merupakan hak cipta dari Larson (2016). For your information, buku Larson (2016) is highly recommended.

Berdasarkan konsep yang bernama Aturan Kosinus (The Law of Cosines), diperoleh

\[\require{cancel} \begin{align} \lVert \mathbf{v} - \mathbf{u} \rVert^2 &= \lVert \mathbf{u} \rVert^2 + \lVert \mathbf{v} \rVert^2 - 2 \lVert \mathbf{u} \rVert \lVert \mathbf{v} \rVert \cos \theta \\ \Longleftrightarrow (v_1 - u_1)^2 + (v_2 - u_2)^2 &= u_1^2 + u_2^2 + v_1^2 + v_2^2 - 2 \lVert \mathbf{u} \rVert \lVert \mathbf{v} \rVert \cos \theta \\ \Longleftrightarrow \cancel{v_1^2} - 2 v_1 u_1 + \cancel{u_1^2} + \cancel{v_2^2} - 2 v_2 u_2 + \cancel{u_2^2} &= \cancel{u_1^2} + \cancel{u_2^2} + \cancel{v_1^2} + \cancel{v_2^2} - 2 \lVert \mathbf{u} \rVert \lVert \mathbf{v} \rVert \cos \theta \\ \Longleftrightarrow u_1 v_1 + u_2 v_2 &= \lVert \mathbf{u} \rVert \lVert \mathbf{v} \rVert \cos \theta \\ \Longleftrightarrow \cos \theta &= \frac{u_1 v_1 + u_2 v_2}{\lVert \mathbf{u} \rVert \lVert \mathbf{v} \rVert}. \tag{1}\label{eq:final-eq} \end{align}\]

Pembilang dari pecahan di ruas kanan dari Persamaan \eqref{eq:final-eq} merupakan hasil kali titik (dot product) dari $\mathbf{u}$ dan $\mathbf{v}$ sehingga Persamaan \eqref{eq:final-eq} dapat ditulis menjadi

\[\begin{equation} \cos \theta = \frac{\mathbf{u} \centerdot \mathbf{v}}{\lVert \mathbf{u} \rVert \lVert \mathbf{v} \rVert}. \end{equation} \tag{2}\label{eq:dot-product}\]

Jadi dapat disimpulkan bahwa Persamaan \eqref{eq:dot-product} menjelaskan hubungan antara hasil kali titik (dot product) antara 2 vektor dan sudut yang dibentuk oleh keduanya.